GROUPES (mathématiques) - Représentation linéaire des groupes

GROUPES (mathématiques) - Représentation linéaire des groupes

Développée d’abord comme moyen de classification des différentes apparences du même groupe G comme groupe de transformations linéaires, la théorie des représentations linéaires est devenue un des outils les plus puissants pour l’étude de la structure de G. En particulier, les caractères irréductibles d’un groupe fini G, introduits pour mieux classer les représentations linéaires, sont vitaux pour la théorie moderne des groupes simples.

1. Représentation des groupes

À chaque système mathématique S est associé son groupe de symétries (ou d’automorphismes) (S). On considère ces groupes (S) comme étant concrets. Une représentation R d’un groupe quelconque G comme groupe de symétries de S est un homomorphisme 靖 料 R size=1^靖 de G dans le groupe concret (S). Elle donne une réalisation de la loi de composition abstraite de G comme loi de composition concrète dans (S).

La théorie des représentations cherche les conséquences, pour les deux structures S et G, de l’existence d’une représentation R, et les utilise pour démontrer des théorèmes qui n’ont quelquefois rien à voir avec les représentations; par exemple, le théorème de Feit et Thompson: tout groupe d’ordre impair est résoluble. Seules les relations entre S et G étant intéressantes, la tendance moderne est de les définir directement et de supprimer le groupe (S) et l’homomorphisme R. Voici, sur un exemple, comment on procède.

Une opération d’un groupe G sur un ensemble E est une loi de composition externe, envoyant tout élément 靖 de G et tout élément x de E sur un élément 靖x de E, et suppose que cette loi satisfait aux conditions:

pour tout x dans E,

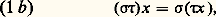pour tout 靖, 精 dans G et tout x dans E, où 靖精 est le produit dans G, et 1 l’élément neutre de G. Ces conditions impliquent que, pour tout 靖 de G, l’application R size=1^靖: x 料 靖x est bijective de E sur E, c’est-à-dire que R size=1^靖 est une permutation sur l’ensemble E. Et l’application 靖 料 R size=1^靖 est un homomorphisme de G dans le groupe (E) des permutations sur E (que l’on peut considérer comme les symétries de E). L’opération de G sur E détermine donc une représentation R de G comme groupe de symétries de E. En fait, la représentation et l’opération ne sont que deux façons de voir la même chose, car la première détermine la seconde par la relation 靖x = R size=1^靖(x ), pour tout 靖 de G et tout x de E.

Une représentation linéaire d’un groupe G est une représentation de G comme groupe de symétries d’un espace vectoriel. Rappelons qu’un espace vectoriel V sur un corps K est un groupe additif muni d’une loi de composition externe, qui envoie tout élément de K et tout élément v de V sur un élémentv de V, et qui est telle que les combinaisons linéaires¹v ¹ + ... +ⁿ v ⁿ d’éléments v ¹, ..., v ⁿ de V à coefficients¹, ...,ⁿ dans K obéissent aux règles ordinaires de calcul. Une opération linéaire de G sur V est une opération de G sur l’ensemble V, satisfaisant à la condition de linéarité:

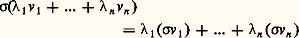pour tout 靖 de G, tout¹, ...,ⁿ de K, et tout v ¹, ..., v ⁿ de V. Chaque application R size=1^靖: v 料 靖v est alors une transformation linéaire bijective de V sur lui-même, et l’homomorphisme 靖 料 R size=1^靖 est une représentation linéaire de G sur V. On dit alors que V est un G-espace.

On dit que deux représentations 靖 料 R size=1^靖 et 靖 料 R size=1^靖 size=1 sur des espaces vectoriels V et V sont équivalentes (ou isomorphes) s’il existe un isomorphisme linéaire de V sur V tel que R size=1^靖 = 﨏^-1 獵 R size=1^靖 size=1^獵 﨏 pour tout 靖 捻 G, ce qui équivaut à 﨏 獵 R size=1^靖 = R size=1^靖 size=1^獵 﨏.

Il y a une autre façon, souvent utile, de considérer les représentations linéaires. Supposons que l’espace vectoriel V ait une base finie v ¹, ..., v ^d , c’est-à-dire que tout élément v de V ait une expression unique: v =¹v ¹ + ... +^d v ^d , comme combinaison linéaire des éléments v ¹, ..., v ^d de la base, à coefficients¹, ...,^d dans K. Pour tout élément 靖 de G, il existe alors des éléments uniques 見^ij ( 靖) dans K tels que:

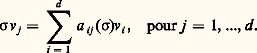La d 憐 d matrice, A ( 靖) = ( 見^ij ( 靖)), détermine la transformation linéaire R size=1^靖 par les équations ci-dessus. Les conditions (1) équivalent à dire que l’application A : 靖 料 A ( 靖) est un homomorphisme du groupe G dans le groupe GL(d , K) de toutes les matrices d 憐 d dont le déterminant n’est pas nul.

On peut donc regarder les représentations linéaires ou les opérations linéaires comme des homomorphismes dans GL(d , K).

Cette façon de voir facilite la définition du caractère 﨑^V du G-espace V. C’est la fonction de G dans K dont la valeur 﨑^V( 靖) est la trace , Tr(A ( 靖)), de la matrice A ( 靖):

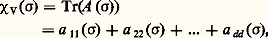pour tout 靖 de G.

La trace de A ( 靖) est indépendante du choix de la base v ¹, ..., v ^d et ne dépend que de la transformation linéaire R 靖. Le caractère 﨑^V est donc déterminé par l’opération. Dans certains cas importants, la réciproque est vraie, c’est-à-dire que l’opération de G sur V est déterminée par le caractère 﨑^V (cf. infra ).

Il faut noter la propriété suivante du caractère 﨑^V, qui découle de l’équation Tr(AB ) = Tr(BA ) pour des matrices A et B :

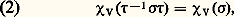pour tout 靖, 精 dans G.

On dit que deux éléments, 靖 et 福 de G sont conjugués s’il existe un élément 精 de G tel que 福 = 精^-1 靖精. Les classes d’équivalence pour cette relation de conjugaison s’appellent les classes de conjugaison de G. La condition (2) signifie donc que chaque caractère 﨑^V est constant sur chaque classe de conjugaison de G.

2. Théorie des représentations linéaires d’un groupe fini

La théorie classique trouvée par G. Frobenius, W. Burnside, et I. Schur dans la période 1890-1910 est la base de toutes les généralisations modernes. Cette théorie s’applique aux représentations linéaires d’un groupe fini G sur des espaces vectoriels de dimensions finies (c’est-à-dire ayant une base finie) sur le corps C des nombres complexes.

On cherche, d’abord, à classer les G-espaces, à des isomorphismes près. Un G-espace V est G-isomorphe à un G-espace U s’il existe une application linéaire bijective f de V sur U qui conserve les opérations de G: f ( 靖v ) = 靖f (v ), pour tout 靖 dans G, et tout v dans V, c’est-à-dire si les représentations linéaires sont équivalentes.

L’outil principal de la classification des opérations linéaires de G sur des espaces vectoriels V est la décomposition des espaces V en somme directe de sous-espaces stables. Un sous-espace de V est un sous-ensemble U, qui est fermé pour la formation de combinaisons linéaires d’éléments; U est donc lui-même un espace vectoriel avec, pour lois de composition, les restrictions des lois de composition de V. Le sous-espace U est stable par G s’il est fermé pour l’opération de G sur U, c’est-à-dire si 靖u appartient à U pour tout 靖 dans G et tout u dans U. Dans ce cas, la restriction à U de l’opération de G sur V est une opération linéaire de G sur U. Soit U¹, ..., U^k des sous-espaces stables de V. On dit que V est la somme directe U¹ 簾 ... 簾 U^k des Uⁱ , si tout élément v de V a une expression unique de la forme:

où u ⁱ appartient à Uⁱ pour i = 1, ..., k.

Les éléments u ¹, ..., u ^k sont les composantes de v pour la décomposition V = U¹ 簾 ... 簾 U^k . La correspondance: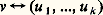

est une bijection de V sur le produit cartésien U¹ 憐 ... 憐 U^k ; les lois de composition de V et l’opération de G sur V se calculent à partir des structures des Uⁱ par les relations:

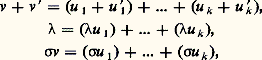où appartient au corps, 靖 au groupe, et où v est un élément de V ayant comme composante les éléments u ¹, ..., u ^k . La décomposition V = U¹ 簾 ... 簾 U^k donne donc une analyse de la structure de V au moyen de celles des Uⁱ .

Si G opère sur un espace vectoriel U 0, et s’il n’y a aucun sous-espace stable par G, sauf U et0, on dit que le G-espace U est irréductible. La classification des opérations linéaires d’un groupe fini G sur des espaces vectoriels V de dimension finie sur le corps C des nombres complexes est contenue dans les deux énoncés suivants:

(3a ) l’espace V a au moins une décomposition: V = U¹ 簾 ... 簾 U^k , en somme directe de sous-espaces stables et irréductibles U¹, ..., U^k ;

(3b ) si V = U ¹ 簾 ... 簾 U ^l est une autre telle décomposition, alors l = k et, après une permutation convenable des indices, Uⁱ est G-isomorphe à U ⁱ , pour i = 1, ..., k .

Pour tout G-espace irréductible W, on définit la multiplicité , m (W dans V), de W dans V. C’est le nombre des indices i = 1, ..., l pour lesquels W est G-isomorphe à Uⁱ . À cause de (3 b ), cette multiplicité est indépendante de la décomposition V = U¹ 簾 ... 簾 U^k . Donc deux G-espaces V et V sont isomorphes si, et seulement si:

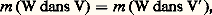pour tout G-espace irréductible W.

Frobenius découvrit une méthode très simple de calcul des multiplicités m (W dans V) en utilisant les caractères. On définit un produit hermitien (f |g )^G sur l’espace vectoriel Fct(G, C) de toutes les fonctions de G dans C par:

pour tout f et g dans Fct(G, C), où g ( 靖) désigne le complexe conjugué de g ( 靖) et |G| est l’ordre de G, c’est-à-dire le nombre d’éléments dans le groupe fini G. Si W et U sont deux G-espaces irréductibles de dimension finie sur G, Frobenius a démontré les relations d’orthogonalité suivantes, pour leurs caractères 﨑^W et 﨑^U:

si W est G-isomorphe à U;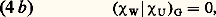

si W n’est pas G-isomorphe à U.

La décomposition, V = U¹ 簾 ... 簾 U^k , entraîne pour les caractères la relation:

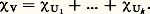On a donc, d’après les relations d’orthogonalité (4), la formule suivante pour la multiplicité de W dans V:

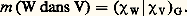On voit que le caractère 﨑^V détermine les multiplicités m (W dans V). Le G-espace V est donc déterminé à un isomorphisme près par son caractère 﨑^V.

Les relations d’orthogonalité (4) montrent que les caractères irréductibles (les caractères des G-espaces irréductibles) distincts sont des fonctions linéairement indépendantes sur le groupe fini G. Il n’y a donc qu’un nombre fini 﨑¹, ..., 﨑^c de tels caractères. On peut alors montrer que le nombre c des caractères irréductibles de G est égal au nombre des classes de conjugaison de G.

Soit H un sous-groupe de G. Tout G-espace V est, par restriction, un H-espace V^H. Le caractère de cet H-espace est la restriction 﨑^H du caractère 﨑 du G-espace V au sous-groupe H. Donc la restriction 﨑 料 﨑^H est une application des caractères de G dans ceux de H. Frobenius découvrit une application, allant en sens inverse, envoyant tout caractère 﨏 de H sur le caractère induit 﨏^G de G défini par:

pour tout 靖 de G, où la sommation sur l’ensemble vide est nulle par définition. Frobenius a démontré la loi de réciprocité :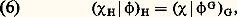

pour tout caractère 﨑 de G et tout caractère 﨏 de H.

On peut calculer les caractères irréductibles de G en utilisant les caractères induits: on part de certains sous-groupes H de G, et de certains caractères connus 﨏 de H. À l’aide de (5), on calcule les caractères induits 﨏^G, qui sont, comme tous les caractères, des combinaisons linéaires a ¹ 﨑¹ + ... + a ^c 﨑^c à coefficients entiers a ¹, ..., a ^c des caractères irréductibles 﨑¹, ..., 﨑^c de G. On cherche alors un nombre suffisant de caractères 﨏^G, de telle manière qu’ils engendrent le groupe additif X(G) de toutes ces combinaisons linéaires de 﨑¹, ..., 﨑^c . Il faut donc trouver les éléments:

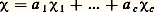de X(G) tels que:

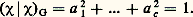Un tel élément est forcément de la forme 梁 﨑ⁱ , où i = 1, ..., c . Comme 﨑ⁱ (1) 礪 0, on peut déterminer le caractère 﨑ⁱ .

Cette méthode est justifiée, car R. Brauer a montré que X(G) est en fait engendré par les caractères induits 﨏^G, où 﨏 parcourt la famille de tous les caractères linéaires (c’est-à-dire irréductibles de degré 1) des sous-groupes H de G. On peut même se restreindre aux sous-groupes H qui sont nilpotents. Un caractère linéaire 﨏 d’un sous-groupe H est simplement un homomorphisme 靖 料 﨏( 靖) de H dans le groupe multiplicatif du corps C. Ces caractères sont donc faciles à calculer.

3. Les généralisations

La théorie classique, exposée ci-dessus, a été au fil des années généralisée de plusieurs façons. L’une d’elles consiste à remplacer le corps C des nombres complexes par un autre corps K. Si le corps K est de caractéristique zéro, ou p (l’entier p étant un nombre premier qui ne divise pas l’ordre fini |G| de G), la théorie des représentations linéaires de G sur les espaces vectoriels de dimension finie sur K se réduit facilement à la théorie classique des caractères complexes de G, et l’on n’obtient aucune notion nouvelle. Par contre, si la caractéristique p de K est un nombre premier qui divise l’ordre |G|, on trouve une nouvelle famille de représentations irréductibles et de caractères de G, les caractères modulaires . L’étude de ces caractères modulaires et de leurs relations avec les caractères complexes, due surtout à R. Brauer, a permis de trouver, pour ces derniers, des lois et identités nouvelles. Plusieurs théorèmes importants sur les groupes simples n’ont pu être démontrés que grâce à la théorie de ces caractères.

Une autre famille de généralisations de la théorie classique concerne les représentations unitaires continues d’un groupe topologique sur un espace de Hilbert. Un groupe topologique G est un groupe muni d’une topologie par rapport à laquelle la multiplication et l’inversion sont des applications continues. Un espace hilbertien V (cf. espace de HILBERT) est un espace vectoriel sur les nombres complexes C muni d’un produit hermitien (u | v ) (c’est-à-dire une application de V 憐 V dans C telle que l’application u 料 (u | v ) est linéaire pour tout v dans V, (u | v ) = (v | u ) pour tout u et v dans V, et (u | u ) est un nombre réel strictement positif pour tout u 0 dans V) et complet pour la norme 瑩v 瑩 = (v | v )^1/2 définie par ce produit hermitien. Une opération linéaire de G sur V est continue si l’application ( 靖, u , v )( 靖v | u ) est continue en tant qu’application de G 憐 V 憐 V dans C. Elle est unitaire si elle conserve le produit hermitien ( 靖v | 靖v ) = (u | v ) pour tout 靖 dans G et tout u , v dans V. On dit, dans ce cas, que V est un G-espace de Hilbert.

Lorsque le groupe topologique G est compact , la théorie est très semblable à la théorie classique. L’espace V admet alors une décomposition en somme orthogonale:

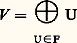d’une famille F de sous-espaces stables et irréductibles U. C’est-à-dire que les U sont des sous-espaces fermés de V, deux à deux orthogonaux pour le produit hermitien (u | v ), et tout élément v de V admet une décomposition unique:

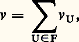en une somme convergente en norme de ses composantes v ^U appartenant à U. Toute autre telle décomposition:

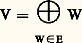est équivalente à la première, en ce sens qu’il existe une application bijective f de E sur F et, pour tout W de E, une application linéaire bijective g de W sur U = f (W) qui conserve les opérations de G et les produits hermitiens sur les deux sous-espaces W et U. Donc V est déterminé à un isomorphisme près par les multiplicités des G-espaces de Hilbert irréductibles W dans V, c’est-à-dire le nombre de sous-espaces U appartenant à F, tels que U soit G-isomorphe à W.

On peut montrer que toute représentation unitaire continue irréductible d’un groupe compact est de dimension finie. Un groupe compact G possède donc des caractères irréductibles . Ces caractères satisfont aussi aux relations d’orthogonalité (4), où le produit hermitien ( 﨑 | 﨏)^G est défini par:

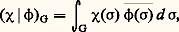l’intégrale étant prise par rapport à la mesure de Haar normalisée (cf. INTÉGRATION ET MESURE, chap. 3):

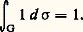Lorsque le groupe G n’est pas compact, la théorie est beaucoup moins nette. Au lieu de décomposer V en sommes orthogonales, il faut le décomposer en intégrales orthogonales de G-espaces irréductibles. De telles décompositions, quand elles existent, ne sont pas nécessairement uniques. Les représentations irréductibles peuvent être de dimension infinie, et donc ne pas avoir de caractères. En général, tout devient très compliqué. Il y a néanmoins une théorie assez bonne pour les représentations des groupes classiques qui sont importants en mécanique quantique.

4. Applications aux groupes finis

Les caractères irréductibles 﨑¹, ..., 﨑^c d’un groupe fini G forment un outil très puissant dans l’étude de G. On considère leurs valeurs comme des invariants numériques de G, invariants qui doivent satisfaire à plusieurs conditions fortes, comme les relations d’orthogonalité, et qui sont liés à la structure algébrique de G. On combine ces conditions et ces relations pour montrer des théorèmes parfois surprenants sur G.

On utilise d’abord les caractères pour trouver des sous-groupes distingués de G. Pour i = 1, ..., c , soit Wⁱ un G-espace ayant 﨑ⁱ pour caractère; on appelle noyau de 﨑ⁱ , le sous-groupe distingué Ker( 﨑ⁱ ) formé de tous les 靖 de G opérant trivialement sur Wⁱ par 靖w = w , pour tout w dans Wⁱ . Il est important de noter que ce sous-groupe distingué est caractérisé par les valeurs de 﨑ⁱ : c’est l’ensemble de tous les éléments 靖 de G tels que 﨑ⁱ ( 靖) = 﨑ⁱ (1).

Il n’y a qu’un seul caractère 﨑ⁱ tel que Ker( 﨑ⁱ ) = G, le caractère trivial 﨑¹ dont les valeurs sont 﨑¹( 靖) = 1 pour tout 靖 de G. Pour tout caractère non trivial 﨑ⁱ , i 閭 2, il existe un élément 靖 de G tel que 﨑ⁱ ( 靖) 﨑ⁱ (1).

On peut aussi montrer que, pour tout élément 靖 1 de G, il existe au moins un caractère non trivial 﨑ⁱ tel que 﨑ⁱ ( 靖) 﨑ⁱ (1).

Une connaissance très grossière des valeurs des caractères de G peut permettre de prouver l’existence d’un sous-groupe distingué K qui soit non trivial (K 1, K G). Il suffit de trouver un seul élément 靖 1 et un seul caractère non trivial 﨑ⁱ tel que 﨑ⁱ (1) = 﨑ⁱ ( 靖). Le sous-groupe K = Ker( 﨑ⁱ ) est alors un sous-groupe distingué non trivial.

On s’intéresse aux relations entre la structure des sous-groupes de G et les caractères de G. Une de ces relations a trait aux ensembles à intersections triviales. Un tel ensemble S est un sous-ensemble d’un sous-groupe H, appelé normalisateur de S, dont les conjugués 靖^-1S 靖 satisfont à:

si 靖 appartient à H;

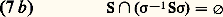si 靖 est dans G mais non dans H.

Voici un exemple d’un tel ensemble S: pour tout 靖 de G, on désigne par Rac( 靖) l’ensemble de tous les 精 de G qui sont racines de 靖 (il existe n tel que 精ⁿ = 靖). Rac( 靖) est un ensemble à intersections triviales, et le sous-groupe H est le normalisateur du sous-groupe cyclique 麗 靖 礪 engendré par 靖. C’est le groupe formé de tous les éléments 福 de G, tels que 福^-1 麗 靖 礪 福 = 麗 靖 礪.

Soit 﨏¹, ..., 﨏^c les caractères irréductibles de H. On désigne par X(H | S) le groupe additif formé des combinaisons linéaires:

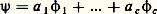(à coefficients entiers a ⁱ ) qui s’annulent hors de S. La fonction induite 祥^G, définie par (5), appartient alors au groupe X(G) formé des combinaisons linéaires à coefficients entiers des 﨑¹, ..., 﨑^c . Les conditions (7) et la formule (5) entraînent:

pour tout 靖 dans S et tout 祥 dans X(H | S).

En combinant cette équation avec la loi de réciprocité (6), on trouve que l’application 祥 料 祥^G est une isométrie X(H | S) 料 X(G), c’est-à-dire que l’on a: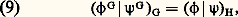

pour tout 﨏 et 祥 dans X(H|S).

Frobenius fut le premier à utiliser cette isométrie. Il considéra le cas où S est égal au sous-groupe H moins l’élément neutre 1. On désigne par K le sous-ensemble de tous les éléments 精 de G qui n’appartiennent à aucun conjugué 靖^-1S 靖 de S. Le théorème de Frobenius dit que l’ensemble K est un sous-groupe distingué de G. On appelle groupe de Frobenius tout groupe G possédant un sous-groupe H différent de1 et de G, ayant la propriété énoncée dans le théorème de Frobenius. Le sous-groupe distingué K s’appelle le noyau de Frobenius (cf. GROUPES FINIS).

La théorie des caractères exceptionnels est basée sur l’isométrie (9). Supposons que 﨏ⁱ et 﨏^j soient deux caractères irréductibles distincts de H tels que 﨏ⁱ 漣 﨏^j appartienne à X(H | S). On a alors: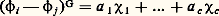

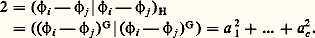pour certains entiers a ¹, ..., a ^c. L’isométrie (9) et les relations d’orthogonalité (4) donnent:

Mais les a ⁱ sont des entiers. Ils sont donc tous nuls, sauf deux d’entre eux, a ⁱ et a ^j, qui valent 梁 1. Si a ⁱ = a ^j = 梁 1, on a:

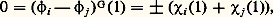ce qui est impossible, car les degrés 﨑ⁱ (1) et 﨑^j(1) sont des entiers strictement positifs. On a donc:

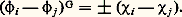On dit que 﨑ⁱ et 﨑^j sont les caractères exceptionnels de G correspondant à 﨏ⁱ et 﨏^j . À cause de (5), ces deux caractères sont égaux en dehors des conjugués de S. Sur ces conjugués, leur différence est déterminée par (8). Ce type de résultat intervient, par exemple, dans la démonstration par Feit et Thompson de leur célèbre théorème: «Tout groupe d’ordre impair est résoluble.» Feit et Thompson utilisent la théorie des caractères exceptionnels pour des isométries qui généralisent (9).

Encyclopédie Universelle. 2012.